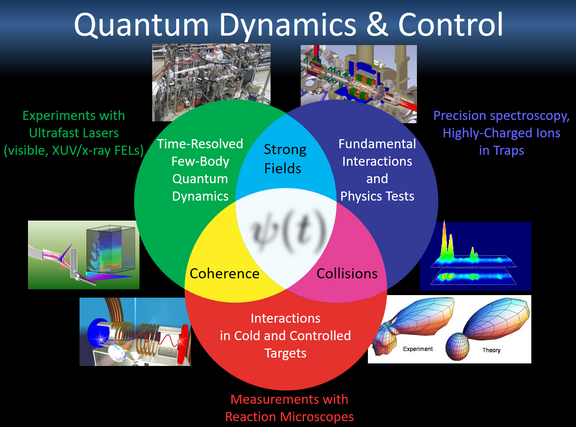
Measurement and Inter-/Back-/Re-/Action at the Origin of Motion
"Where motion comes to life”
Motion plays a pivotal role in life, the universe, and everything.
- Why do things start to move?
- How fast are the smallest movements?
- When does quantum motion turn classically visible?
- In what way can we steer movements?
- What is time?
In our division's → research we use “fast” bright light and multi-dimensional measurement techniques to illuminate these and further questions evolving around the dynamical quantum world.
News
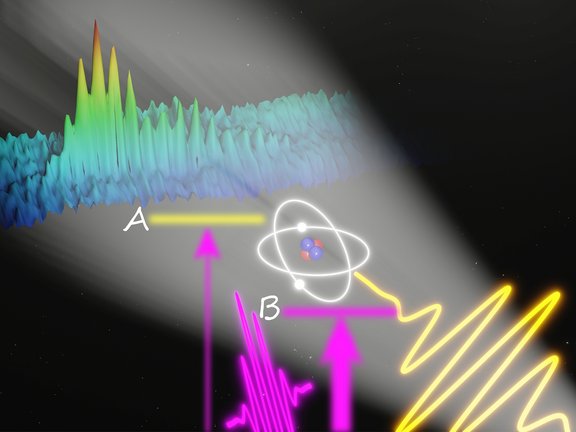
Bringing weak transitions to light
A new general concept for laser-induced enhancement of faint spectral lines is experimentally demonstrated for quasi-forbidden transitions in helium.…
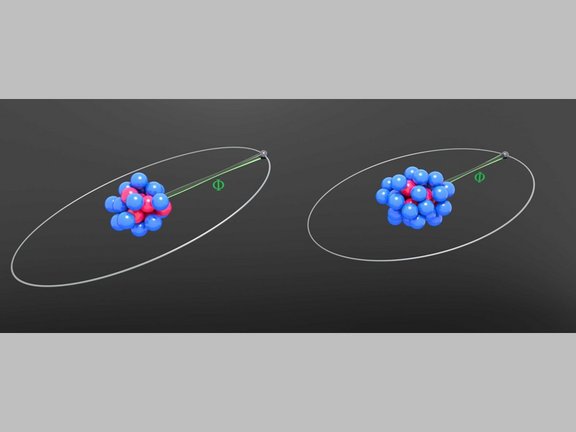
Joint effort in the search for new physics
As part of an international collaboration MPIK researchers carried out highly precise measurements as well as calculations on atomic transitions in…
DPG Dissertation prize for Viviane Schmidt
This year's dissertation prize of the German Physical Society (DPG), section atoms, molecules, quantum optics and photonics, was awarded to Dr.…