High-Energy Quantum Electrodynamics
Quantum electrodynamics (QED) was formulated in its final form by Dyson, Feynman, Schwinger, and Tomonaga, and it is the most successful among the physical theories in terms of agreement with experimental data. The validity of QED has been thoroughly scrutinized with great precision at high energies by means of particle accelerators and in bound atomic systems by means of highly-charged ions. Modern high-power laser facilities are becoming an alternative tool to test QED in the highly nonlinear regime and in the so-called strong-field sector (see the review A. Di Piazza et al., Rev. Mod. Phys. 84, 1177 (2012)). In fact, laser fields are produced outside the region where their interaction with charged particles as electrons and positrons occurs, such that processes are exclusively referable to the electromagnetic interaction without the complications brought about, for example, by a highly-charged nucleus.
In the strong-field QED regime elementary QED processes occur in the presence of background electromagnetic fields with amplitudes effectively of the order of Ecr=1.3 × 1016 V/cm and Bcr=4.4 × 1013 G. A laser beam with an electric (magnetic) field amplitude of the order of Ecr (Bcr) would have a peak intensity of Icr=4.6 × 1029 W/cm2. In the presence of such strong electromagnetic fields fascinating phenomena take place and become sizable. Among them we quote spontaneous electron-positron pair production from vacuum, harmonic generation in the collision of two strong laser beams in vacuum, and the fact that the vacuum becomes a birefringent and dichroic medium. All these phenomena have their ultimate origin in the pure quantum interaction among electromagnetic fields also in vacuum, this interaction being mediated mainly by virtual electron-positron pairs (vacuum fluctuations, see the figure). Indeed, unlike Maxwell's equations in vacuum, the quantum equations describing the evolution of electromagnetic fields in vacuum are highly nonlinear. Another genuinely quantum effects, which becomes sizable when electrons and positrons experience in their rest frame electromagnetic fields of the order of Ecr and Bcr, the so-called photon recoil, i.e., the energy and momentum carried away from the charge by the photon at the moment of emission, which are also proportional to the Plnck constant.
In this context high-power optical laser facilities that are already or soon available represent a unique tool to investigate experimentally the predictions of QED. Petawatt laser facilities are already operating and have already reached the record intensity of 1023 W/cm2. Moreover, intensities of the order of 1024-1025 W/cm2 are envisaged at the Extreme Light Infrastructure (ELI) and at the Exawatt Center for Extreme Light Studies (XCELS). Although even the intensities available at future laser facilities will lie well below the critical intensity, the strong-field QED regime can be effectively entered by employing ultrarelativistic electron beams or photon beams with energies much larger than the electron rest energy. The reason is that the Lorentz- and gauge-invariant parameter controlling strong-field QED effects in the laser intensity, which charged particles involved in the reaction experience in their rest frame. Now, available accelerator facilities and the recent accelerator technique known as laser wake-field acceleration provide electron beams with energies beyond the GeV threshold. Thus, it can be easily ascertained that present-day electron and laser technology already allow in principle to enter the strong-field QED regime.
We investigate some main aspects of QED in the presence of intense laser fields:
- The nonlinear dielectric properties of the quantum vacuum. QED predicts that the presence of a strong electromagnetic field in the vacuum changes the dielectric properties of the vacuum itself, rendering it a birefringent medium. In order to reveal these properties strong electromagnetic fields are needed of the order of the critical fields. Alternatively, we have proposed to employ photons with energies much larger than the electron rest energy and to use the process of nonlinear Breit-Wheeler pair production to detect the vacuum-polarization effects arising when the high-energy photons cross a region, where a strong laser field is present.
- High-energy QED processes in intense laser fields. QED processes where high-energy electron or photon beams collide with intense laser fields are of great interest both theoretically and experimentally. The corresponding probabilities show a very complex and highly nonlinear dependence on the laser field parameters giving the possibility of testing QED with high accuracy. Among these processes we have studied single and double nonlinear Compton scattering and nonlinear Breit-Wheeler pair production, as well as nonlinear trident pair production.
- Radiative corrections in intense laser fields. Experimental campains like the E320 at SLAC and LUXE at DESY aim at testing strong-field QED at high precision by employing monoenergetic electron beams produced by a conventional accelerator and controlled laser beams. In order to compare theory and experiments it is timely to compute radiative corrections in strong-field QED, which we have started by computing the vertex-correction in an arbitrary plane-wave field. We have also investigated the different dependence on the energy scale of radiative corrections at asymptotically large particles energies and laser intensity, a topic related to the so-called Ritus-Narozhny conjecture.
- Radiation-reaction effects in intense laser fields. In the presence of intense laser fields, the interaction of an electron with its own electromagnetic field can change significantly the electron dynamics (radiation reaction). We have recently studied the problem of radiation reaction both classically (Landau-Lifshitz equation) and quantum mechanically (the quantum origin of radiation reaction) and we have put forward experimental setups potentially allowing for measuring such effects.We have collaborated with experimental groups which have observed effects of quantum radiation reaction with intense lasers and strong crystalline fields.
- Electromagnetic cascades. If two or more laser beams collide in a region where bound or free electrons are present, the latter are violently accelerated emitting high-energy photons. These in turn interact with the laser beams transforming into electron-positron pairs, which again can emit high-energy photons. If the intensities of the colliding lasers is initially sufficiently high (indicatively of the order of 1024 W/cm2 or higher), an avalanche or cascade of electrons, positrons, and photons is initiated. These systems offer the quite unique possibility of observing collective quantum effects in the ultrarelativistic regime, as opposed to the well-known one at very low energies like Bose-Einstein condensates.
- Gravitational radiation by laser-driven charges. Accelerated electric charges emit also gravitational radiation. The properties of the latter are significant different from those of electromagnetic radiation as, for instance, also the electromagnetic field produced by the charge then emits graviational radiation. Nevertheless, we have shown that at the tree level the emission amplitude of a graviton and of a photon by an electron driven by a strong plane wave are proportional to each other.
People
- Antonino Di Piazza (Group Leader)
- Giulio Audagnotto (Post Doc)
- Sapan Karki (Post Doc, University of Rochester)
- Misha Lopez-Lopez (Post Doc, University of Rochester)
- Adrian Hosak (PhD Student, University of Rochester)
- Reshad Rahman (PhD Student, University of Rochester)
- Lorenzo Tamburino Ventimiglia di Monteforte (PhD Student)
- Thomas de Vos (PhD Student, University of Rochester)
No available positions at the moment. Excellent candidates are invited to directly contact Antonino Di Piazza at any time.
Selected projects
Radiation by a laser-driven flying-focus electron wave packet

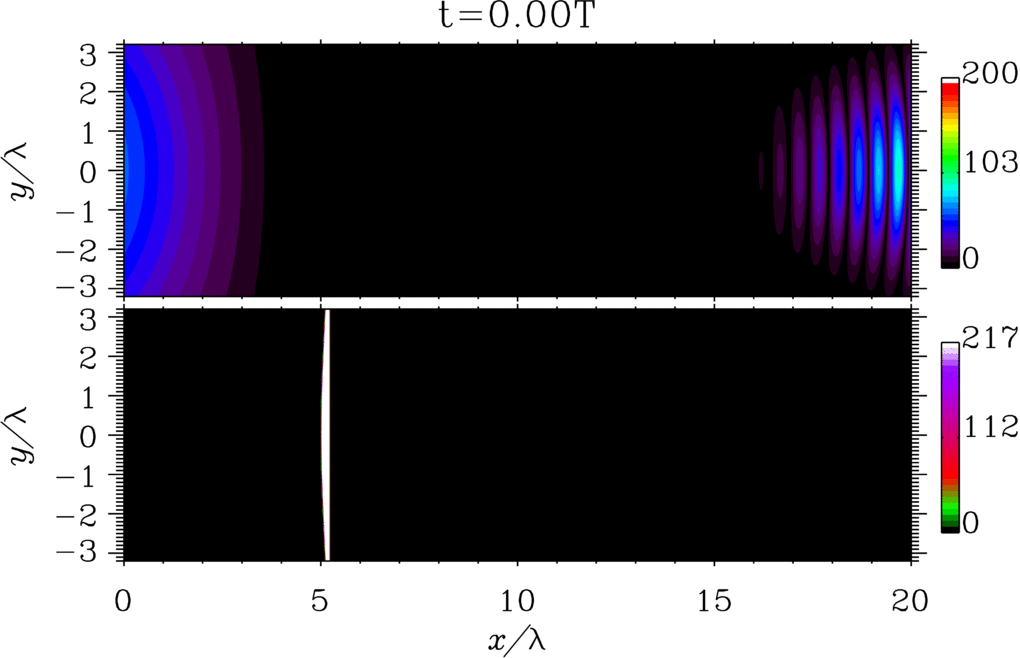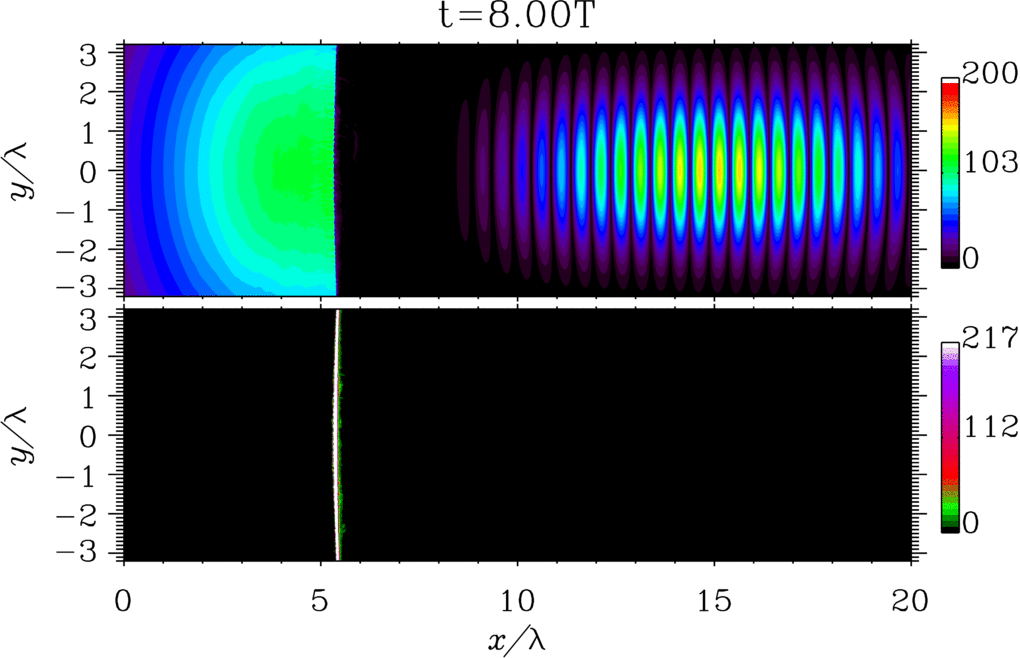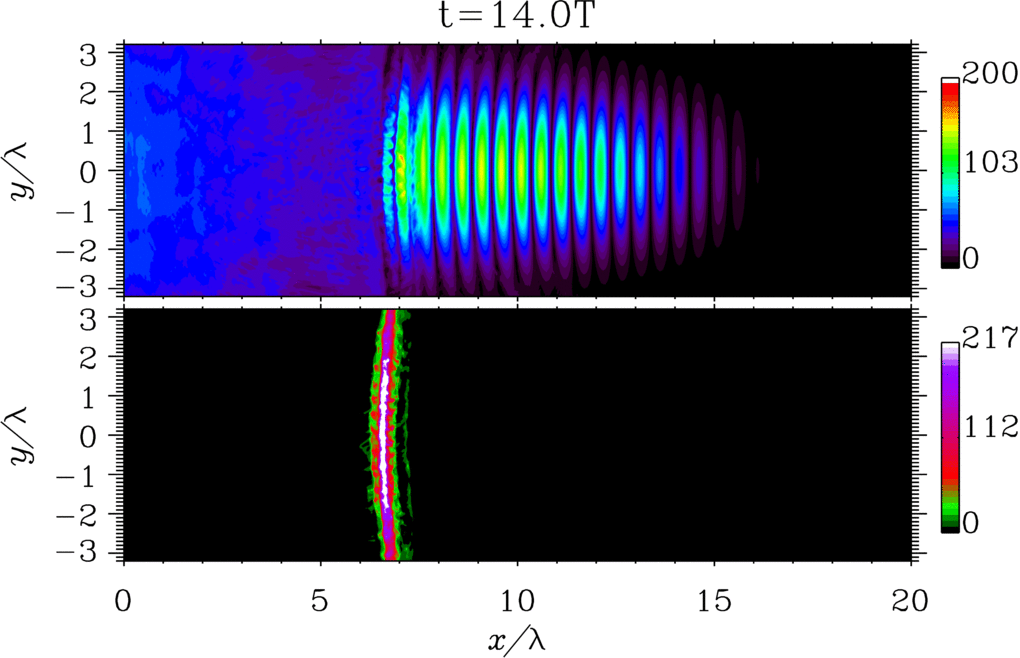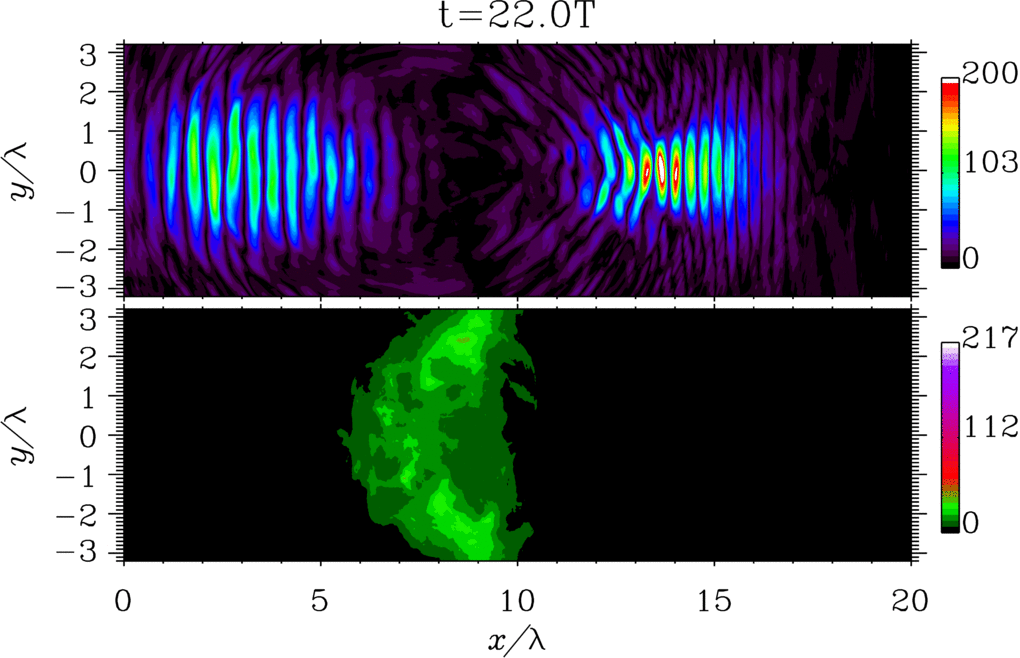
The possibility of generating light with peculiar spacetime structures is attracting a lot of attention because `structured light'' can open new and unique frontiers of light-matter interaction [1,2]. A notable example of structured light is represented by flying-focus beams, i.e., beams whose focal velocity is independent of the group velocity and can be controlled externally [3]. In Ref. [4] we have analyze the problem of a flying-focus-like electron wave packet in the case of the dressed Dirac equation in the presence of an arbitrary plane-wave electromagnetic field. We have found a new analytical solution of the dressed Dirac equation, which exactly describes a focused electron wave packet, whose focus corresponding to each momentum component of the wave packet moves at the speed of light in the opposite direction of the subluminal average velocity of the wave packet. Also, we have computed the probability of nonlinear single Compton scattering and shown how the angular properties of the emitted radiation are modified as compared to the standard case of an incoming electron with definite momentum (see the figure).
[1] O. V. Angelsky, A. Y. Bekshaev, S. G. Hanson, C. Y. Zenkova, I. I. Mokhun, and J. Zheng, Front. Phys. 8, 114 (2020).
[2] J. Wang and Y. Liang, Front. Phys. 9, 263 (2021).
[3] D. H. Froula, D. Turnbull, A. S. Davies, T. J. Kessler, D. Haberberger, J. P. Palastro, S.-W. Bahk, I. A. Begishev, R. Boni, S. Bucht, J. Katz, and J. L. Shaw, Spatiotemporal control of laser intensity, Nat. Photonics 12, 262 (2018).
[4] A. Di Piazza, M. Formanek, D. Ramsey, and J. P. Palastro, Radiation by a laser-driven flying-focus electron wave packet, Phys. Rev. D 110, 116010 (2024).
Charged particle beam transport in a flying focus pulse with orbital angular momentum
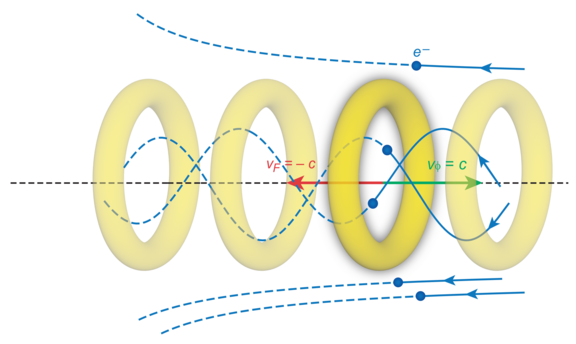
In a flying focus (FF) laser pulse the velocity of the focus of the pulse can be controlled and made even larger than the speed of light [1]. In Ref. [2] we have demonstrated the capability of flying focus laser pulses with ℓ=1 orbital angular momentum (OAM) to transversely confine ultrarelativistic charged particle bunches over macroscopic distances while maintaining a tight bunch radius. A FF pulse with ℓ=1 OAM creates a radial ponderomotive barrier that constrains the transverse motion of particles and travels with the bunch over extended distances (see the figure). As compared with freely propagating bunches, which quickly diverge due to their initial momentum spread, the particles cotraveling with the ponderomotive barrier slowly oscillate around the laser pulse axis within the spot size of the pulse. This can be achieved at FF pulse energies that are orders of magnitude lower than required by Gaussian or Bessel pulses with OAM. The ponderomotive trapping is further enhanced by radiative cooling of the bunch resulting from rapid oscillations of the charged particles in the laser field. This cooling decreases the mean-square radius and emittance of the bunch during propagation.
[1] D. H. Froula, D. Turnbull, A. S. Davies, T. J. Kessler, D. Haberberger, J. P. Palastro, S.-W. Bahk, I. A. Begishev, R. Boni, S. Bucht, J. Katz, and J. L. Shaw, Spatiotemporal control of laser intensity, Nat. Photonics 12, 262 (2018).
[2] M. Formanek, J. P. Palastro, M. Vranic, D. Ramsey, and A. Di Piazza, Charged particle beam transport in a flying focus pulse with orbital angular momentum, Phys. Rev. E 107, 055213 (2023).
First-order strong-field QED processes including the damping of particles states
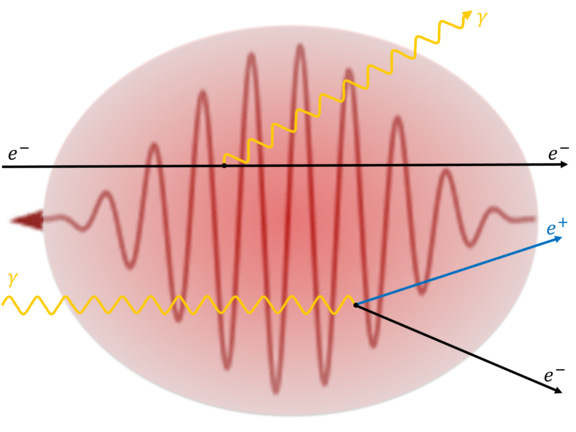
Nonlinear Compton scattering (the emission of a photon by an electron in a plane wave) and nonlinear Breit-Wheeler pair production (the decay of a photon into an electron-positron pair in a plane wave) are first-order processes of strong-field QED (see the figure). When calculating their probabilities from the leading order Feynman diagram it turns out, that they can exceed unity for a plane wave background field with a sufficiently long pulse duration. This of course contradicts the unitarity of the S-matrix and indicates that higher order loop corrections become important in the limit of long pulse length. Indeed, to obtain physical probabilities for arbitrary long phase length of the background pulse one has to perform the resummation over infinitely many higher order one-particle-reducible Feynman diagrams, which contain corrections by the mass- and polarization-operator for the fermion and photon states, respectively. This can be understood as electron/positron (Volkov) and photon states are not stable in the presence of the plane-wave background field but “decay” as electrons/positrons can emit photons and photons can transform into electron-positron pairs. We performed this resummation by using for the fermion and photon states the solutions of the corresponding Schwinger-Dyson equations within the locally constant field approximation and used them to compute the probabilities of nonlinear single Compton scattering and nonlinear Breit-Wheeler pair production, which then include the effects of the decay of electron, positron, and photon states. This decay of the particle states leads to an exponential damping term in the probabilities of single nonlinear Compton scattering and nonlinear Breit-Wheeler pair production [1]. A numerical investigation showed that it is crucial to take into account the damping of the states in order the probabilities to stay always below unity and we observed that the damping factors also scale with the pulse duration of the background field. In the case of nonlinear Compton scattering we have also shown that the total probability of emitting a single photon behaves like a Poissonian distribution for sufficiently low initial electron energies such that the photon recoil is negligible [2].
[1] T. Podszus and A. Di Piazza, First-order strong-field QED processes including the damping of particle states, Phys. Rev. D 104, 016014 (2021).
[2] T. Podszus, V. Dinu and A. Di Piazza, Nonlinear Compton scattering and nonlinear Breit-Wheeler pair production including the damping of particle states, Phys. Rev. D 106, 056014 (2022).
Collisional strong-field QED kinetic equations from first principles
Strong-field QED cascades are systems of electrons, positrons, and photons produced in the collisions of, for example, ultrastrong laser beams [1]. Typically the charged particles are ultrarelativistic and the background electromagnetic field is ultrastrong in the sense that the classical nonlinearity parameter is much larger than unity. This allows to describe the evolution of the cascades by means of local, Vlasov-like kinetic equations [2]. These equations have been written including the basic strong-field QED processes (nonlinear Compton scattering and nonlinear Breit-Wheeler pair production) but they do not include, for example, spin effects or nonlocal effects. In Ref. [3] we have started from nonequilibrium quantum field theory on a closed time path and we have derived the mentioned kinetic equations of strong-field QED using a systematic expansion in the gauge coupling e. The strong field enters the dynamical equations via both quantum Vlasov and collision terms, which we derive to order O(e2). The kinetic equations feature generalized scattering amplitudes that have their own equation of motion in terms of the fermion spectral function. Our approach includes not only nonlinear Compton scattering and nonlinear Breit-Wheeler pair production but also vacuum (Schwinger) pair production, their inverse processes, medium effects, and nonlocal contributions from the field. For the purpose of analytically highlighting limiting cases, we have also considered a plane-wave background field for which it is shown how to recover Furry-picture scattering amplitudes by further assuming negligible occupations numbers.
[1] A. R. Bell and J. G. Kirk, Phys. Rev. Lett. 101, 200403 (2008).
[2] N. V. Elkina, A. M. Fedotov, I. Y. Kostyukov, M. V. Legkov, N. B. Narozhny, E. N. Nerush, and H. Ruhl, Phys. Rev. ST Accel. Beams 14, 054401 (2011).
[3] G. Fauth, J. Berges, and A. Di Piazza, Collisional strong-field QED kinetic equations from first principles Phys. Rev. D 104, 036007 (2021).
One-loop vertex correction in a plane wave
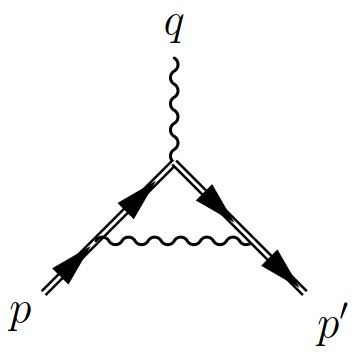
The one-loop mass and polarization operators in the presence of an arbitrary plane wave were computed in the seventies [1,2]. The more complicated vertex correction (see the figure) was computed in the case of a plane wave with zero frequency, i.e., a constant crossed field in Ref. [3]. An important conclusion in Ref. [3] was that at large values of the quantum non-linearity parameter χ the vertex correction is about αχ2/3. In Ref. [4] we have computed the one-loop vertex correction in an arbitrary plane wave and we have in particular investigated its properties under gauge transformations of the plane wave and of the radiation field. Most importantly, by working within the locally constant field approximation, we have found that the scaling αχ2/3 pertains to terms, which finally cancel when one computes physical amplitudes, as they are gauge-dependent.
[1] V. N. Baier, V. M. Katkov, A. I. Milstein, and V. M. Strakhovenko, Sov. Phys. JETP 42, 400 (1976).
[2] V. N. Baier, A. I. Milstein, and V. M. Strakhovenko, Sov. Phys. JETP 42, 961 (1976).
[3] D. A. Morozov, N. B. Narozhny, and V. I. Ritus, Sov. Phys. JETP 53, 1103 (1981).
[4] A. Di Piazza and M. A. Lopez-Lopez, One-loop vertex correction in a plane wave, Phys. Rev. D 102, 076018 (2020).
Approaching the non-perturbative regime of strong-field QED using aligned crystals
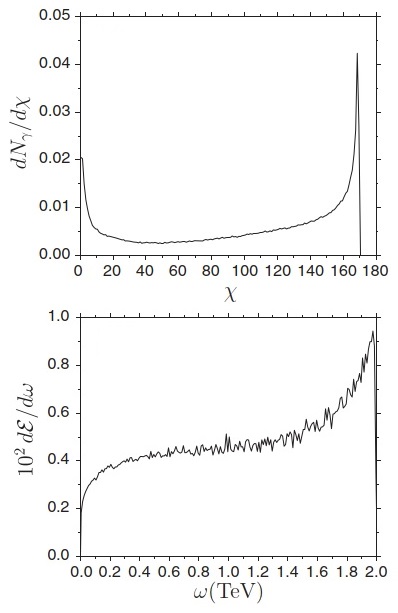
It was conjectured by V. I. Ritus and by N. B. Narozhny that at such high background electromagnetic field that electrons and positrons would experience in their rest frame a field strength of about 1/α3/2 ≈ 1600 times the critical field of QED, the interaction between the electron-positron Dirac field and the photon field would become strong [1,2]. Here, α is the fine-structure constant and in this regime QED would behave as a strongly-interacting theory as QCD. There have been several proposals on how to enter this fully non-perturbative regime of QED by using lasers. In Ref. [3] we have proposed to use ultra-relativistic electrons propagating inside a crystal in the so-called channeling regime to approach this regime. We have shown that channeling radiation by ultrarelativistic electrons with energies of the order of a few TeV on thin tungsten crystals allows one to test the predictions of QED close to the fully non-perturbative regime by measuring the angularly resolved single photon intensity spectrum. The proposed setup featured the unique characteristics that essentially all electrons (1) undergo at most a single photon emission and (2) experience at the moment of emission and in the angular region of interest the maximum allowed value of the field strength, which at 2 TeV exceeds the critical field of QED by more than two orders of magnitude in their rest frame (see the figure).
[1] V. I. Ritus, Sov. Phys. JETP 30, 1181 (1970).
[2] N. B. Narozhny, Phys. Rev. D 20, 1313 (1979).
[2] A. Di Piazza, T. N. Wistisen, M. Tamburini, and U. I. Uggerhøj, Testing strong-field QED close to the fully non-perturbative regime using aligned crystals, Phys. Rev. Lett. 124, 044801 (2020).
Improved local-constant-field approximation for strong-field QED codes
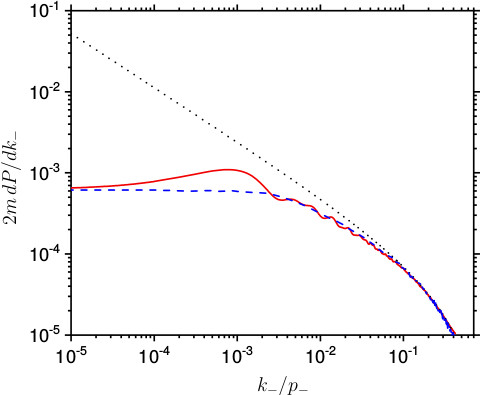
The local-constant field approximation (LCFA) is a powerful and thus widely-used approximation in strong-field QED because it allows to compute transition probabilities in arbitrary background electromagnetic fields starting from the corresponding expressions in a constant crossed field, i.e., a constant electromagnetic field with electric and magnetic fields having the same amplitude and being perpendicular to each other. The LCFA is particularly suitable for strong-field QED in intense laser fields because it is applicable, generally speaking, when the laser field is able to accelerate an electron to untrarelativistic energies already in a single cycle [1]. This condition should imply that a generic strong-field QED process is formed over a distance, called formation length, which is much smaller than the laser wavelength, such that the laser field can be approximated as constant in order to compute the probability of the process itself.
However, we have realized that this condition is insufficient to guarantee the validity of the LCFA for the process of photon emission (nonlinear Compton scattering) in the infrared part of the emission spectrum [2]. The intuitive explanation of this failure is that low-energy photons have relatively large wavelengths such that it is not surprising that at a certain point the background field can no longer be approximated as being constant on the photon formation length.
As a related result, we have found a local method to capture the nonlocal features of the radiation probability for low-energy photons in a way that it can still be efficiently implemented in numerical codes [3]. The virtue of this method can be seen in the figure, which shows photon emission spectra according to a full quantum calculation (solid red curve), to the LCFA (dotted, black curve), and to the method developed in Ref. [3] (dashed blue curve).
[1] V. I. Ritus, J. Sov. Laser Res. 6, 497 (1985).
[2] A. Di Piazza, M. Tamburini, S. Meuren, and C. H. Keitel, Implementing nonlinear Compton scattering beyond the local-constant-field approximation, Phys. Rev. A 98, 012134 (2018).
[3] A. Di Piazza, M. Tamburini, S. Meuren, and C. H. Keitel, Improved local-constant-field approximation for strong-field QED codes, Phys. Rev. A 99, 022125 (2019).
Quantum limitation to the coherent emission of accelerated charges
In classical electrodynamics, accelerated charges emit electromagnetic radiation. By virtue of the superposition principle, the total emitted electromagnetic field is the sum of the fields emitted by each charge [1], whereas the total radiated energy is quadratic in the amplitude of the emitted electromagnetic field. It can be shown that if accelerated charged particles move along sufficiently close trajectories, the total energy emitted scales quadratically with their number.
The process of emission of radiation by charged particles, accelerated by an intense laser field, can be studied at the quantum level within strong-field QED [2]. In this framework the "quantum nonlinearity parameter" generally describes the importance of quantum effects like the photon recoil [2]. In the case of a single emitting charge, when the quantum nonlinearity parameter is much smaller than unity, the predictions of strong-field QED for the emitted energy spectrum agree with the classical ones. One may naively expect the same to hold true for the process of emission of radiation by multiple charges.
By investigating the emission by a two-electron wavepacket in the presence of an electromagnetic plane wave within strong-field QED, we have shown [3] that quantum effects deteriorate the coherence predicted by classical electrodynamics even if the typical quantum nonlinearity parameter of the system is much smaller than unity (see the figure). We explain this result by observing that coherence effects are also controlled by a new quantum parameter which relates the recoil undergone by the electron in emitting a photon to the width of its wave packet in momentum space [3].
[1] J. D. Jackson, Classical Electrodynamics, (Wiley, New York, 1999).
[2] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Rev. Mod. Phys. 84, 1177 (2012).
[3] A. Angioi and A. Di Piazza, Quantum limitation to the coherent emission of accelerated charges, Phys. Rev. Lett. 121, 010402 (2018).
Experimental evidence of quantum radiation reaction in aligned crystals
In classical electrodynamics there is a century old outstanding problem, the so-called radiation reaction problem [1]. When a charge, an electron, for definiteness, is accelerated, it emits radiation, and this should be taken into account in the description of the subsequent motion of the electron. The original attempt at a solution of this problem, resulted in the so-called Lorentz-Abraham-Dirac equation, which is a 3rd order differential equation and can be shown to conflict with the principle of causality. More recently this has been amended by a scheme of reduction of order, leading to the so-called Landau-Lifshitz equation, which is free of these problems [2].
The quantum mechanical picture of the problem of radiation reaction under certain approximations is that of an electron consecutively emitting several photons. For radiation reaction effects to be treated quantum mechanically, the electron should be driven by strong electromagnetic fields, such that the quantum nonlinearity parameter &chi, i.e., the ratio of the field acting on the charge in the electron's instantaneous rest-frame and the Schwinger critical electric (magnetic) field strength Ecr (Bcr), is of the order of unity or larger.
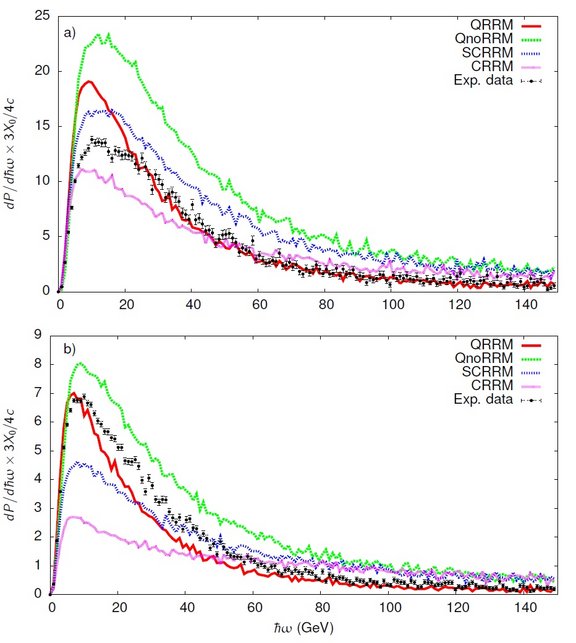
In the experiment described in [3] we achieved such strong fields by channeling positrons with energy of 180 GeV through a Silicon crystal. In addition, the crystal is thick enough that on the order of 20 photons are emitted per incoming positron. Now, the calculation of the emission spectrum corresponding to several photons is in general a formidable task. Therefore one must rely on an approximation, the so-called constant crossed field approximation, where the emission of many photons can be calculated knowing only the emission spectrum of the single photon emission process. In our experiment, however, the conditions for this approximation to be applicable are not completely fulfilled, and we see some deviations between theory and experiment due to this in the case of a crystal with 3.8-mm thickness (see the part a of the figure). The results in the 10.0-mm case theory and experiments agree to a better degree (see the part b of the figure). In both cases, we refer to the theoretical results obtained by treating quantum mechanically the emission of several photons (red lines), whereas the theoretical models corresponding to the other curves are described in detail in [3].
[1] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Rev. Mod. Phys. 84, 1177 (2012).
[2] L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields (Elsevier, Oxford, 1975).
[3] T. N. Wistisen, A. Di Piazza, Helge V. Knudsen, and U. I. Uggerhøj, Experimental evidence of quantum radiation reaction in aligned crystals, Nat. Commun. 9, 795 (2018).
High-energy vacuum birefringence and dichroism in an ultrastrong laser field
In the realm of classical electrodynamics the electromagnetic field experiences no self-interaction in vacuum. According to QED, however, a finite photon-photon coupling is induced by the presence of virtual charged particles in the vacuum [1]. For low-frequency electromagnetic fields such vacuum polarization effects are described by the Euler-Heisenberg Lagrangian density [2]. The Euler-Heisenberg Lagrangian density predicts that the vacuum resembles a birefringent medium. Despite having been predicted long time ago, vacuum birefringence has not been observed in a laboratory experiment yet, due to the smallness of the photon-photon coupling.
As the light-by-light scattering cross section attains its maximum at the pair-production threshold [2], it is natural to consider high-energy photons to probe vacuum birefringence. In [3] we have derived how a generally polarized probe photon beam is influenced by both vacuum birefringence and dichroism. Furthermore, we have considered an experimental scheme to measure these effects in the high-energy regime, where the Euler-Heisenberg approach breaks down. The scheme is based on Compton backscattering to produce polarized gamma photons [2] and exploits pair production in matter to determine the polarization state of the probe photon after it has interacted with a strong laser pulse.
By analyzing the consecutive stages of this type of experiment, we have shown that for vacuum birefringence the required measurement time is reduced by two orders of magnitude if a circularly polarized probe photon beam is employed. Assuming conservative experimental parameters, we demonstrate that the verification of the strong-field QED prediction for vacuum birefringence is feasible with an average statistical significance of 5σ on the time scale of several days at upcoming 10-PW laser facilities. We also show that vacuum dichroism and anomalous dispersion in vacuum (see the figure) could be accessible at these facilities.
[1] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Rev. Mod. Phys. 84, 1177 (2012).
[2] V. B. Berestetskii, E. M. Lifshitz, and L. P. Pitaevskii, Quantum Electrodynamics (Elsevier, Oxford, 1982).
[3] S. Bragin, S. Meuren, C. H. Keitel, and A. Di Piazza, High-energy vacuum birefringence and dichroism in an ultrastrong laser field, Phys. Rev. Lett. 119, 250403 (2017).
Nonlinear Breit-Wheeler pair production in a tightly focused laser beam
The electric field strength where such nonlinear QED effects become sizable identifies the "strong-field QED" regime and is given by the so-called Schwinger field: Ecr=1.3 × 1016 V/cm. Due to the extremely large value Ecr, present and upcoming lasers have to be tightly focused in space (and in time) in order to aim at values comparable with Ecr. Nonetheless, the value of Ecr exceeds by about four orders of magnitudes presently available laser-field amplitudes [1,2]. However, the effective field at which a QED process occurs is that experienced by participating charged particles in their rest frame. Thus, by employing ultrarelativistic electron (positron) beams, the strong-field QED regime can effectively be probed also nowadays in principle.
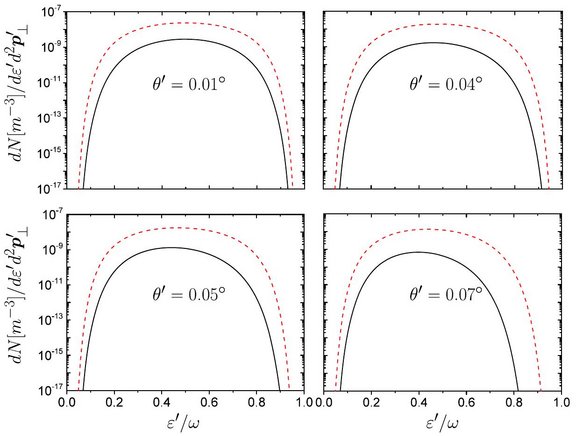
Now, all systematic approaches to investigate analytically strong-field QED processes rely on approximating the laser beam as a plane wave, which allows for solving the Dirac equation exactly but which cannot account for laser spatial focusing effects. In [3] we have realized that in order to enter the strong-field QED regime at present and upcoming laser facilities, the electrons have to be so highly relativistic that the Wentzel-Kramers-Brillouin (WKB) approximation can be employed (at the next-to-the-leading order) to solve analytically the Dirac equation in the presence of a background laser field practically of arbitrary space-time shape. The electron wave functions obtained in this way open the possibility of investigating analytically and in a systematic way strong-field QED processes in the presence of a tightly focused laser beam of complex and realistic space-time shape by employing the so-called Furry picture. Indeed, we have already determined analytically the energy spectrum and the angular distribution of the electron-positron pairs produced in the collision of a photon bunch with an intense and tightly-focused laser beam (nonlinear Breit-Wheeler pair production) [4]. As a byproduct, by means of a numerical implementation of the analytical results, we have proven that the inclusion of the laser tight focusing is essential for a correct quantitative estimate of the number of created pairs (see the figure).
[1] V. I. Ritus, J. Sov. Laser Res. 6, 497 (1985).
[2] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Rev. Mod. Phys. 84, 1177 (2012).
[3] A. Di Piazza, Phys. Rev. Lett. 113, 040402 (2014).
[4] A. Di Piazza, Nonlinear Breit-Wheeler pair production in a tightly focused laser beam, Phys. Rev. Lett. 117, 213201 (2016).
Nonlinear single Compton scattering of an electron wave packet
According to QED, an electron interacting with an intense laser field can emit a photon, while exchanging many photons with the laser field itself [1]. This process is indicated as nonlinear single Compton scattering.
Due to the progress in the technology of ultrashort few-cycles laser pulses [2], there are already many envisaged laser facilities that will soon allow testing QED in the high-intensity regime and probe nonlinear single Compton scattering.
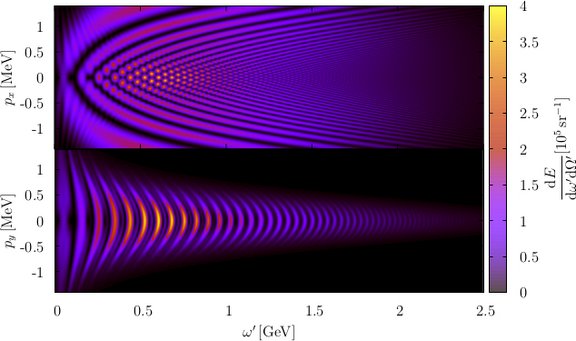
In particular, motivated by the fact that electrons are produced in general as wave packets and that they are localized to some extent in beams, we focused on the effect that a certain energy width of the initial wave packet has on the emitted energy spectrum of nonlinear single Compton scattering [3]. We have shown that due to energy-momentum conservation laws and on-shell conditions one does not find quantum interference in the spectrum of the different momentum components of the wave packets, such that the spectrum itself is indeed only the average of the spectra corresponding to electrons having initially different but definite momenta. Moreover, we have analyzed to which extent the indeterminacy of the initial momentum of the electron alters the photon spectra (see the figure). The most typical effect of the indetermination of the initial state is to wash out the highly oscillating structure of the spectrum obtained for electrons with definite momentum, as well as the broadening the angular emission range. At a given relative indeterminacy, we have shown that the one on the electron energy affects the photon spectra more significantly than that on the laser photon energy.
[1] V. I. Ritus, J. Sov. Laser Res. 6, 497 (1985).
[2] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Rev. Mod. Phys. 84, 1177 (2012).
[3] A. Angioi, F. Mackenroth, and A. Di Piazza, Phys. Rev. A 93, 052102 (2016) (Editors' Suggestion).
High-energy recollision processes of laser-generated electron-positron pairs
In quantum field theory in vacuum, Feynman diagrams with particle loops correspond to quantum fluctuations, with the extension, for example, of an electron-positron loop being limited to the Compton space-time scale by the Heisenberg uncertainty principle [1]. However, the situation changes profoundly in the presence of a strong laser field [2]. In fact, above the threshold for real electron-positron pair production the laser field can transfer enough energy to the electron and the positron in the loop to significantly increase the space-time extension of the loop itself. Correspondingly, the intermediate electron and positron can be accelerated over a macroscopic distance (i.e. of the order of the laser wavelength) rather than over a microscopic one (i.e. of the order of the Compton wavelength), and gain an energy corresponding to many laser photons. A careful analysis of the trajectory of an electron (positron) inside a linearly polarized plane-wave field reveals that for certain initial conditions the high-energy electron and positron can recollide and annihilate providing energy and momentum for secondary reactions as in an "electron-positron vacuum collider".
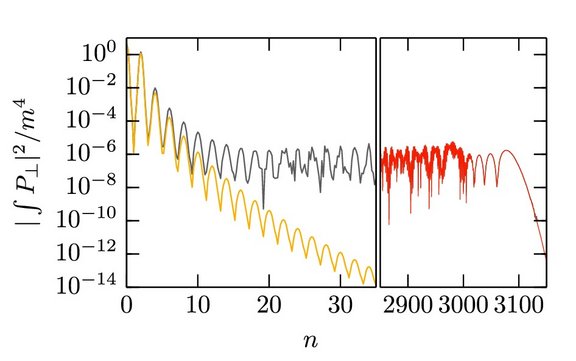
The simplest Feynman diagram which contains an electron-positron loop is the leading-order contribution to the polarization operator [1]. The complete evaluation of the square of the polarization operator (see the gray curve in the figure) shows that both vacuum fluctuation-type processes (yellow curve), corresponding to the creation and the annihilation of the electron-positron pair within the same microscopic formation region, and recollision-type processes (red curve), corresponding to the creation and the annihilation of the electron-positron pair being separated by a macroscopic distance of the order of the laser wavelength, contribute to the probability of absorbing n laser photons [2]. The recollision contribution is responsible of the existence of a large plateau region in the spectrum, in close analogy to high-harmonic generation in atomic physics.
[1] V. B. Berestetskii, E. M. Lifshitz, and L. P. Pitaevskii, Quantum Electrodynamics (Elsevier, Oxford, 1982).
[2] S. Meuren, K. Z. Hatsagortsyan, C. H. Keitel and A. Di Piazza, Phys. Rev. Lett. 114, 143201 (2015).
Generation of neutral and high-density electron-positron pair plasmas in the laboratory
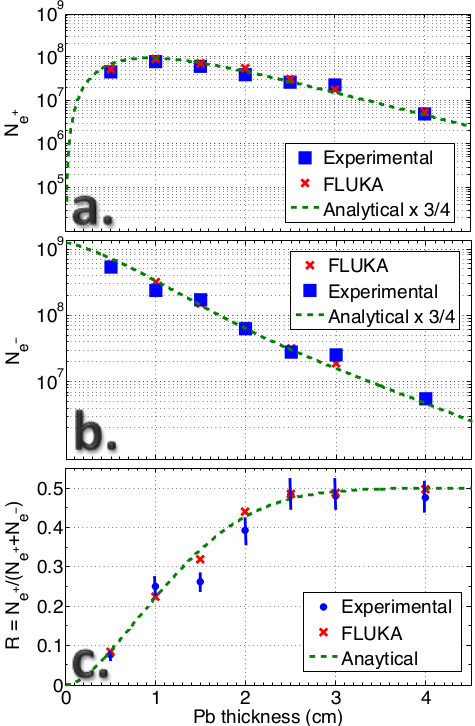
Electron-positron plasmas are emitted as ultrarelativistic jets in different astrophysical scenarios under extreme conditions, like during gamma-ray bursts. In collaboration with Dr. Gianluca Sarri and Prof. Matt Zepf, from the Queen's University Belfast, we have generated such a unique state of matter in the laboratory [1] in the collision of an ultrarelativistic electron beam with a Lead solid target. As a consequence of the complex interaction of the electron beam with the nuclei and the electrons in the target, an ultra-relativistic electron-positron bunch was observed on the rear side of the solid target, with a fraction of electrons and positrons depending on the target thickness (see the figure). The density of the bunch was found to be sufficiently high that its skin-depth resulted smaller than the bunch transverse size, allowing for collective, i.e., plasma effects.
We have identified the main mechanisms responsible for the production of the electron-positron bunch and described its formation and evolution inside the solid target. A simple model has been put forward, which, among all possible interactions occurring inside the solid target, includes only two fundamental quantum electrodynamical processes: 1) bremsstrahlung of electrons and positrons, and 2) electron-positron photoproduction of photons, both occurring in the presence of the screened electromagnetic field of the solid target atomic nuclei. Analytical estimations and numerical integrations of the corresponding kinetic equations agree extremely well with the experimental results on the relative population of electrons and positrons in the generated beam (see in particular the blue dots and the green dashed line in the part c of the figure). Absolute electron and positron yields were also very well predicted by the model apart from an overall factor of the order of unity. In order to reproduce theoretically also more detailed features of the experimental results, Dr. Gianluca Sarri has employed the available fully integrated particle physics Monte-Carlo simulation code FLUKA (see in particular the red crosses in the figure), which among others also includes electron-electron and electron-positron interactions, atomic scattering and other breaking mechanisms, together with high-energy processes like muon--anti-muon pair production.
Plasma-based generation and control of a single few-cycle high-energy ultrahigh-intensity laser pulse
A wide range of novel studies in nonlinear optics as well as the major new regimes of extreme field physics require laser pulses which simultaneously exhibit the following three key features: few-cycle duration, high-energy and ultrahigh intensity. Already in nonrelativistic atomic physics, it has been demonstrated that quantum processes can be controlled by manipulating the pulse shape of few-cycle laser pulses [1]. In order to achieve the same goal also in the ultrarelativistic regime and in the realm of strong-field QED, few-cycle laser pulses with tunable carrier-envelope phase (CEP) are required with peak intensities largely exceeding 1020 W/cm2 [2]. In [3] we put forward the concept of a laser-boosted solid-density parabolic relativistic "mirror", interacting with a superintense counterpropagating laser pulse, to generate a CEP tunable few-cycle pulse with multi-joule energy and peak intensity exceeding 1023 W/cm2 (see the figure). It is found that a heavy and therefore relatively slow mirror should be employed to maximize the intensity and the energy of the reflected pulse. This counterintuitive result is explained with the larger reflectivity of a heavy foil, which compensates for its lower relativistic Doppler factor. Moreover, since the counterpropagating pulse is ultrarelativistic, the foil is abruptly dispersed and only the first few cycles of the counterpropagating pulse are reflected. Our multi-dimensional particle-in-cell simulations show that a single few-cycle, multi-petawatt laser pulse with several joule of energy and with peak intensity exceeding 1023 W/cm2 can be generated already employing next-generation high-power laser systems. In addition, the carrier-envelope phase of the generated few-cycle pulse can be tuned provided that the carrier-envelope phase of the initial counterpropagating pulse is controlled.
[1] F. Krausz and M. Ivanov, Rev. Mod. Phys. 81, 163 (2009).
[2] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Rev. Mod. Phys. 84, 1177 (2012).
[3] M. Tamburini, A. Di Piazza, T. V. Liseykina, and C. H. Keitel, Phys. Rev. Lett. 113, 025005 (2014).
Stochasticity effects in quantum radiation reaction
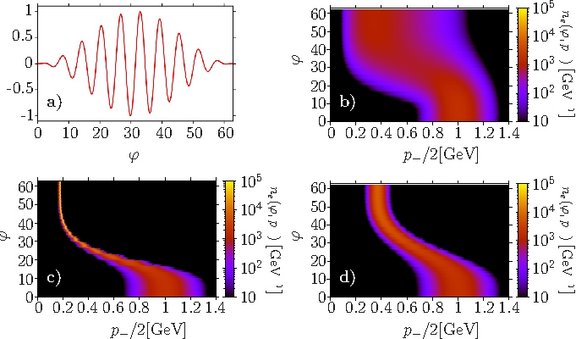
When an electron is accelerated by an electromagnetic field, the emission of photons carrying away energy and momentum leads to a modification of the electron trajectory. In the realm of classical electrodynamics, this backreaction is called radiation reaction (RR) and is described by the so-called Landau-Lifshitz (LL) equation. Furthermore, in the ultra-relativistic, "nonlinear moderately quantum" regime, where nonlinear effects in the laser field and nonlinear QED effects are important, whereas pair production can still be neglected, RR can be described as the incoherent emission of many photons. In [2] we studied the head-on collision of an intense laser pulse with an ultrarelativistic electron beam by means of a kinetic approach. The figure shows that the emission of radiation broadens the initial electron distribution drastically for the full quantum calculations. On the other hand, the classical calculations according to the LL equation predict a strong narrowing of the electron energy spectra due to RR effects. Moreover, if the classical radiation intensity is substituted by its quantum analogue [3] in the classical equation, the energy width of the electrons would still be decreased during the interaction with the laser pulse. The peculiar difference of RR in the classical and the quantum regime can be understood by the importance of the stochastic nature of photon emission in the latter. While in classical electrodynamics the effects of stochasticity in the radiation process are negligible and, in turn, the electron dynamics can be characterized by deterministic equations, it becomes crucial in the quantum regime. Even in the case, where quantum effects are relatively small, the classical kinetic equations must be modified by an additional stochastic term inducing a spread of the electron energy distribution [2].
[1] L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields, Elsevier, Oxford (1975).
[2] N. Neitz and A. Di Piazza, Phys. Rev. Lett. 111, 054802 (2013).
[3] V. I. Ritus, J. Sov. Laser Res. 6, 497 (1985).
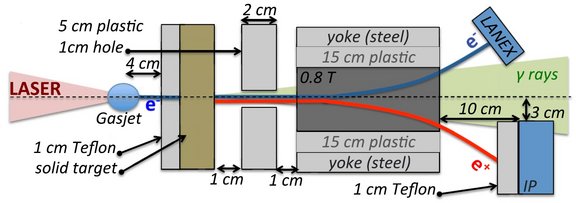
Table-top laser-based source of femtosecond, collimated, ultrarelativistic positron beams
Ultra-relativistic, highly-collimated positron beams have been generated so far by employing large-scale electron accelerators. The electron beams produced by the accelerator collides with a solid target (typically gold or lead), generating on the rear side electron-positron bunches, whose oppositely-charged constituents can be later separated. The main mechanism responsible of such process is the emission of photons via bremsstrahlung by the incoming electrons deflected by the ions in the solid target and the consequent transformation of the bremsstrahlung photons into electron-positron pairs when still in the target. In collaboration with the experimental group lead by Dr. Gianluca Sarri and Prof. Matt Zepf at the Queen's University Belfast, we have generated an incoming monoenergetic electron beam via laser wake-field acceleration (see the figure). After letting it interact with a thin, solid target, we succeeded in producing for the first time positron beams of short (~ 30 fs) duration, with ultra-relativistic energies (>100 MeV), and with a narrow angular distribution (~ 3 mrad) in a table-top setup. The possibility of generating such high-energy lepton beams is of central importance for astrophysics due to their similarity to jets of long gamma-ray bursts.