When a light wave hits a double-slit, a characteristic pattern of bright and dark stripes appears behind the obstacle, generated by constructive or destructive superposition (interference) of the light waves, depending on the direction of the observed light.
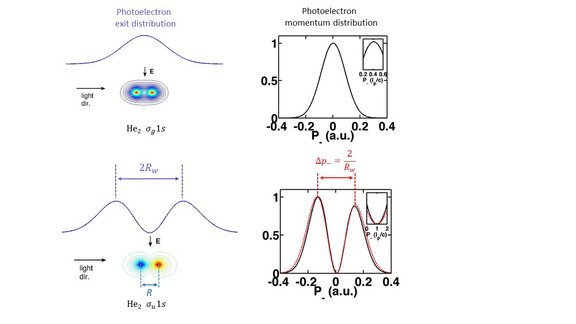
In quantum physics, this phenomenon is also found in matter waves, e.g. electrons released from a diatomic molecule by photoionization. Here, the characteristic quantity is the distance between the atoms in the molecule (bond length).
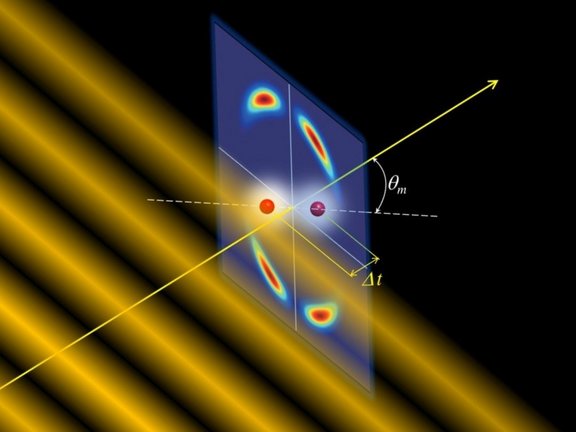
Besides the structure of the molecule, on closer inspection the time difference of the light wave fronts hitting the atoms also plays a role if, e.g., the molecular axis is tilted to the light path (see Fig. 2).
The high electromagnetic light field of the laser rips the electron out of the molecule. This happens even at field strengths that are actually too low, with the electron "tunneling out" of the molecule against the electrical attraction of the positively charged nuclei - the quantum tunnelling effect.
In a new study [1], Pei-Lun He and Karen Hatsagortsyan from Christoph Keitel's theory division at the MPI for Nuclear Physics in Heidelberg have now investigated in detail how the effects mentioned (light travel time through the molecule and interference of electron waves) behave during tunnel ionization and under which conditions this would be observable experimentally.
In addition, there is the momentum that a single light particle transfers to the entire molecule in the ionization process – here, physicists speak of non-dipole contributions (see Fig. 2). Typically, these occur at high photon energies (ultraviolet or x-rays). However, in intense infrared laser fields, this effect also appears when a high number of low-energy photons interact simultaneously with the electron. This was preceded by a work [2] on how the transferred momentum of the absorbed light is distributed between the released electron and the ion remaining behind in atomic photoionization.
For the molecular case, the researchers now found as an essential result that the distance of the "tunnel exits" replaces the bond length - with corresponding consequences for the interference patterns. For noble gas dimers (e.g. He2), the time difference in the momentum distribution of the electrons parallel to the light-propagation direction is significant and depends on the ground state of the dimer (see Fig. 2).
Original publications:
[1] Nondipole Time Delay and Double-Slit Interference in Tunneling Ionization
Pei-Lun He, Karen Z. Hatsagortsyan, and Christoph H. Keitel
Phys. Rev. Lett. 128, 183201 (2022), DOI: 10.1103/PhysRevLett.128.183201
[2] Nondipole Coulomb sub-barrier ionization dynamics and photon momentum sharing
Pei-Lun He, Michael Klaiber, Karen Z. Hatsagortsyan, and Christoph H. Keitel
Phys. Rev. A 105, L031102 (2022), DOI: 10.1103/PhysRevA.105.L031102
Group Hatsagortsyan in the Division Keitel at MPIK