Ionic Quantum Dynamics and High-Precision Theory
In atomic systems with high nuclear charges, inner-shell electrons experience extremely high nuclear binding fields. The dynamics of electrons becomes relativistic and also the electronic probability density has a considerate overlap with the nuclear matter. These properties render highly charged ions an ideal tool for basic research in relativistic atomic structure theory, quantum electrodynamics at extreme fields, and nuclear structural contributions. Accurate knowledge of the properties of highly charged ions is also necessary for the diagnostics of hot fusion plasmas and astrophysical plasmas. In few- and many-electron ions, relativistic and nuclear effects are intertwined with large electron correlation contributions. Because of this complex interplay, accurate theoretical calculations are necessary to explain the physical phenomena observed in increasingly accurate experimental spectra.
Besides investigations on transition energies and spectral properties, quantum electrodynamic and nuclear corrections to the bound-electron g factor are calculated. We also study the interaction of intense lasers in the optical as well as the x-ray regime with highly charged ions, and, furthermore, energetic collision, ionization and recombination processes. In theoretical simulations we describe the dynamics of charged particles in strong laser fields and develop efficient laser accelation schemes.
Group members
- Zoltán Harman (group leader)
- Chunhai Lyu (postdoc)
- Bastian Sikora (postdoc)
- Suvam Singh (postdoc)
- Sreya Banerjee (Ph.D. student)
- Eugen Dizer (HiWi student)
- Junis Heiland Hoyo (HiWi student)
- Lorie Turco (student intern)
Recent projects
The g factor of the bound electron

An external static magnetic field gives rise to the Zeeman splitting of an atomic energy level, with a strength characterized by the dimensionless g factor of the state. In the last decades, experimental techniques, in particular, measurements with Penning traps has reached a remarkable precision (see e.g. Ref. [1] and references therein), allowing for novel studies of fundamental physics. These include the test of bound-state quantum electrodynamics (QED) at high orders [1], and the extraction of nuclear properties such as nuclear radii [1] and nuclear magnetic moments [2,3]. Furthermore, physical constants such as the electron mass [4] and the fine-structure constant [5,6] can be determined with high
accuracy from a comparision of experimental data and theoretical results. Recently we have shown that high-precision measurements of the bound-electron g factor can be effectively used to search for physics beyond the standard model [7]: a high-precision comparison of the magnetic moments of two isotopically different neon ions allows to set upper bounds on the coupling strength of massive scalar bosons that might mediate a hypothetical interaction between electrons and nucleons [8].
Electron binding energies in highly charged ions
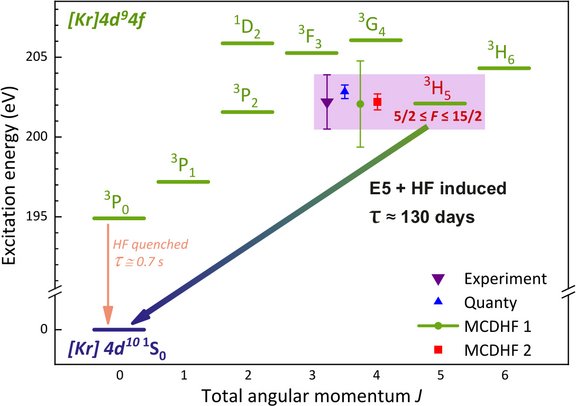
Penning-trap mass spectroscopy has recently enabled a novel determination of binding energies through the comparison of ionic masses. In the first ever direct measurement of an electron binding energy in a heavy highly charged ion, namely of the valence electron in the Rb-like Xe ion, an uncertainty of a few eV has been demonstrated. The experimental value agrees with our result predicted in the framework of the multiconfiguration Dirac-Hartree-Fock method [1]. The collaboration of theory and experiment has also enabled the discovery of ultranarrow ionic transitions, suitable for constructing future atomic clocks: in the Re29+ ion, a long-lived electronic state with an excitation energy of 202 eV was observed via the mass difference of excited and ground-state ions [2]. A further application of such investigations is the determination of the Q value of the β decay of various atomic isotopes, relevant for the determination of the neutrino mass [3]: experimentally, the masses of Re and Os HCI could be determined to high precision, and our calculations have delivered the accurate binding energies of the electrons missing from the neutral atoms.
Correlated relativistic quantum dynamics in resonant recombination processes
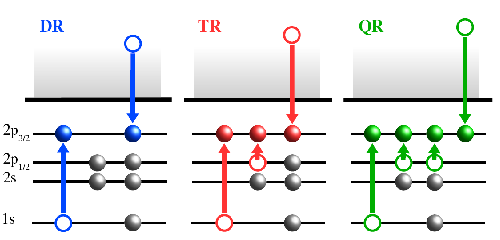
In the process of radiative recombination (RR), a photon is directly emitted by an electron, i.e. it is the time-reverse of the photoelectric effect. Alternatively, in a two-step process, the incoming electron resonantly excites a bound electron during recombination, leading to dielectronic recombination (DR, see Fig.). Furthermore, in some ionic species, the simultaneous excitation of two bound electron may occur. This higher-order process may be termed as trielectronic recombination (TR). These photorecombination processes involving HCI in collisions with energetic electrons are important for a number of applications. In particular, DR is known as a source of the severe energy losses from high temperature plasmas such as magnetically confined fusion plasmas or stellar plasmas, and, thus, a precise quantitative understanding of such phenomena is indispensable. We calculate cross sections and accurate resonance peak positions. These calculations are tested by high-resolution EBIT experiments (see [1-3]), and by experiments at the ESR [4,5] and CRYRING storage rings of the GSI, and the Cryogenic Storage Ring of the MPIK.
Resonant photoionization and photoexcitation of highly charged ions by synchrotron x-rays
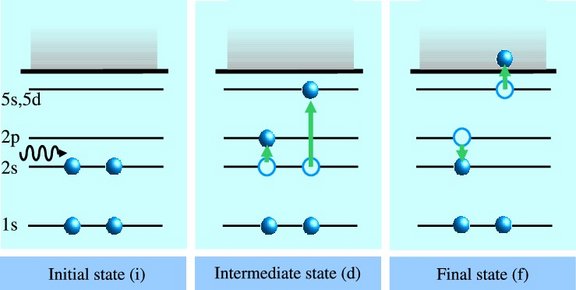
The photoionization (PI) of atomic systems may proceed via a resonant two-step mechanism: In the first step, a photon is absorbed by resonant excitation to an autoionizing intermediate state embedded into the electronic continuum (see Fig.). In the second step, the so-formed state autoionizes. Alternatively, the excited state may decay by the spontaneous emission of a photon. In the case of HCI, the photon energies needed are in the x-ray (short-wavelength) domain. In astrophysics, PI of HCI has been recently observed in high-resolution x-ray spectra of quasars, which display absorption lines due to the presence of HCI in the line of sight. Such data have revealed the hitherto only presumed existence of a tenuous warm-hot intergalactic medium, the so-called WHIM, comprising a large fraction of baryonic matter. For the identification and analysis of absorption lines due to HCI in astrophysical spectra, a large amount of reliable theoretical or experimental PI data is needed. We perform fully relativistic distorted wave calculations of PI and photoexcitation cross sections, transition energies and linewidths, accompanying recent measurements employing electron beam ion traps (EBIT) and synchrotrons as a source of x-ray photons in the keV range [1-3].
Nuclear effects in highly charged ions
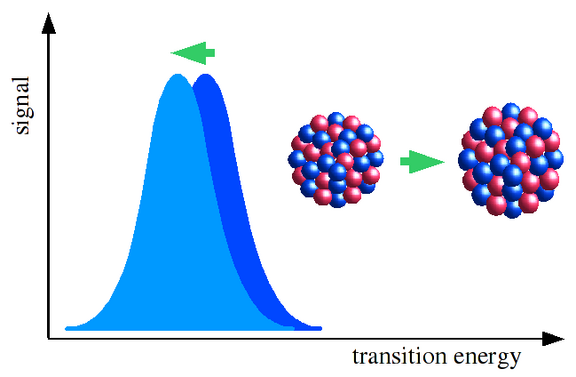
Isotope shift measurements performed in storage rings, combined with our atomic structure calculations, allow one to extract information on the nuclear charge distribution of the isotopes involved and thus about the interplay of forces that act between the nuclear constituents. In a theoretical study, we have analyzed the dependence of electron interaction and QED contributions of the bound-state electronic transition energy on the nuclear size in order to determine the change of nuclear radii corresponding to the isotope shift in three-electron neodymium. Experimental isotope shifts have been measured with the ESR storage ring of the GSI Darmstadt [1]. This approach, based on a close collaboration of theory [2] and experiment, constitutes a novel technique to determine nuclear charge radii. Detailed information on nuclear structure may be also gained by studying the nuclear quadrupole moments along an isotopic chain: in a recent project in collaboration with the CERN-ISOLDE laboratory, quadrupole moments for a broad range of Sn isotopes were extracted from laser spectroscopic hyperfine splitting data with the help of large-scale atomic structure theory [3,4].
The high-precision theory of multiply charged ions has been investigated in EBIT group of our institute. Extensive theoretical studies of the ground-state forbidden magnetic dipole transition in boronlike (five-electron) argon ions have been performed. The mass isotope shift associated with this line have been determined with high accuracy using the EBIT. The wavelengths of the above transition were compared for the isotopes 36Ar and 40Ar. The observed isotope shift has confirmed the relativistic theory of nuclear motional effects in many-body systems [5]. Calculations based on the fully relativistic recoil operator are in excellent agreement with the measured results.
Laser acceleration of charged particles
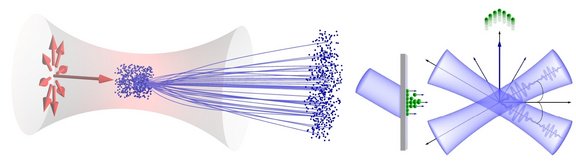
We perform theoretical investigations concerning the strong-field dynamics of ions in order to develop optimal schemes for laser ion acceleration. Laser-accelerated beams may find applications in basic research, medicine, and industry. As an example, cancer hadron therapy requires accelerated ion beams of high energy sharpness and a narrow spatial profile in order to accurately irradiate the tumor while sparing damage from the surrounding healthy tissue. As we have shown in theoretical simulations [1,2], linearly and radially polarized, tightly focused and thus extremely strong laser beams should permit the direct acceleration of light atomic nuclei up to energies that may offer the potentiality for medical applications and may allow one to build more economic cancer treatment facilities. In a different setting employing two identical crossed laser beams [3], ions originating from a laser-plasma process can be post-accelerated to form a beam of high intensity, energy and quality. In recent studies, the acceleration of protons by a chirped laser pulse is simulated using the particle-in-cell method to take into account plasma effects and has been found to be even more efficient than the set-ups described above [4-6]. Finally, the autoresonance laser acceleration of electrons in strong axial magnetic fields is investigated. This scheme is anticipated to yield electron beams with energies up to the 10-GeV regime with an ultrahigh energy resolution when applying multi-petawatt laser pulses [7].
| [1] Y. I. Salamin, Z. Harman, and C. H. Keitel, Phys. Rev. Lett. 100, 155004 (2008) (see also: Informationsdienst Wissenschaft Online; Pro-Physik.de; Photonik) |
| [2] Z. Harman, Y. I. Salamin, B. J. Galow, C. H. Keitel, Phys. Rev. A 84, 053814 (2011) |
| [3] B. J. Galow, Z. Harman, and C. H. Keitel, Opt. Express, 18, 25950 (2010) |
| [4] B. J. Galow, Y. I. Salamin, T. V. Liseykina, Z. Harman, C. H. Keitel, Phys. Rev. Lett. 107, 185002 (2011) |
| [5] Y. I. Salamin, J.-X. Li, B. J. Galow, Z. Harman, C. H. Keitel, Phys. Rev. A 85, 063831 (2012) |
| [6] J. Li, B. J. Galow, C. H. Keitel, and Z. Harman, Appl. Sci. 5, 36 (2015) |
| [7] B. J. Galow, J.-X. Li, Y. I. Salamin, Z. Harman, C. H. Keitel, Phys. Rev. ST Accel. Beams 16, 081302 (2013) |