Theory Division
Theoretical Quantum Dynamics and Quantum Electrodynamics


top row: Ze-an Peng, Zoia Mandrykina, Miriam Gerharz, Aleksandr Boitsov, Giulio Audagnotto, Samuele Montefiori, Christoph Keitel, Sergey Volkov, Michael Quin, Vladimir Yerokhin, Bastian Sikora
second row: Pei-Lun He, Karen Hatsagortsyan, Suvam Singh, Arjit Shankar Banerjee, Matteo Tamburini, Lukas Wolff, Yutong He, Chunhai Lyu, Çağrı Erciyes, Ingmar Kloß, Zoltán Harman
third row: Sibel Babacan, Shikha Bhadoria, Lorenzo Tamburino Ventimiglia di Monteforte, Moritz Thierfeld, Matteo Moretti, Sreya Banerjee, Jörg Evers, Natalia Oreshkina, Igor Valuev, Zewen Sun
bottom row: Minkyung Chun, Robert Horn, André Gontijo Campos, Konstantin Beyer, Morgan Lynch, Cedric Quint, Junis Heiland Hoyo, Hrishikesh Sriman-Narayan
Nachrichten
Joint effort in the search for new physics
As part of an international collaboration MPIK researchers carried out highly precise measurements as well as calculations on atomic transitions in…
Listening to electrons talk: g-factor measurement of lithium-like tin
Researchers from the MPIK present new experimental and theoretical results for the bound electron g-factor in lithium-like tin which has a much higher…
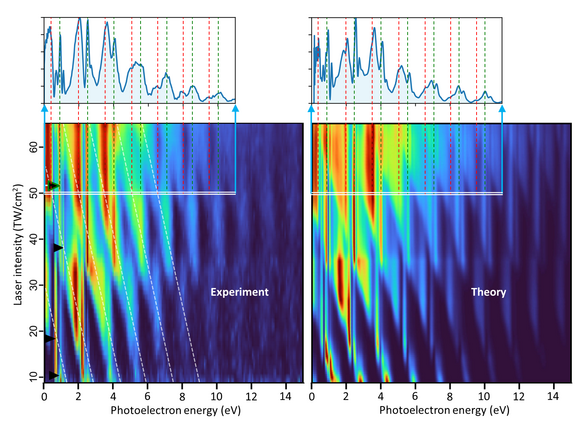
Reverse gear in the quantum tunnel
Under-the-barrier recollision dynamics in strong field ionisation of xenon is revealed both theoretically and experimentally by the theory division at…