Constraining Cosmic Magnetic Fields
January 2023
Magnetic fields have a profound influence on life on Earth. Without the Earth's magnetic field, for example, charged cosmic rays would reach the surface of the Earth is much higher numbers and modify cells in living organisms in a dramatic way. While the human body cannot sense magnetic fields, their strengths can be measured and is given in the units of 'Tesla', named after Austrian-born Engineer Nikolas Tesla. In Astronomy, magnetic field strengths are frequently given in so-called 'cgs-units' of 'Gauss', with 10000 Gauss corresponding to 1Tesla. Near the poles the Earth magnetic field is about 60 micro-Tesla or 0.6 Gauss (G). Moving away from the surface of the Earth, the strength of the magnetic field drops and reaches values of a few nano-Tesla (tens of a micro-Gauss ) at a distance of a few million kilometers from Earth. This weak magnetic field is due to the sun and the solar wind. The magnetic field on the surface of the sun can reach values of up to 0.3 Tesla (3000 G) in Sunspots (see, e.g. the thumbnail image, taken with the trace instrument, image credits: NASA). Magnetic fields have been traced not only in interplanetary space but also in the interstellar medium and are known to thread entire Galaxies. With a variety of techniques the strength of magnetic fields can be measured in structures as large as Mega-parsec. While the magnetic fields within the solar system can be measured directly using space-probes, measurements of magnetic fields in general is rather demanding.Measuring (or even constraining) the strength of the Magnetic field on even larger scales is very important for an understanding of several cosmological questions, but is very difficult to measure these magnetic fields. The technique used in most studies employs the so-called 'Faraday effect'. Linearly polarized electromagnetic waves (radiation, see fig. 1) propagate in a plane unless a magnetic field exists. If the electromagnetic waves propagate through a medium with even a small magnetic field, the orientation of the plane rotates and the amount of rotation depends on the frequency of the electromagnetic radiation. It is a very ambitious technique to measure the frequency dependence of the rotation if the magnetic fields are very weak.
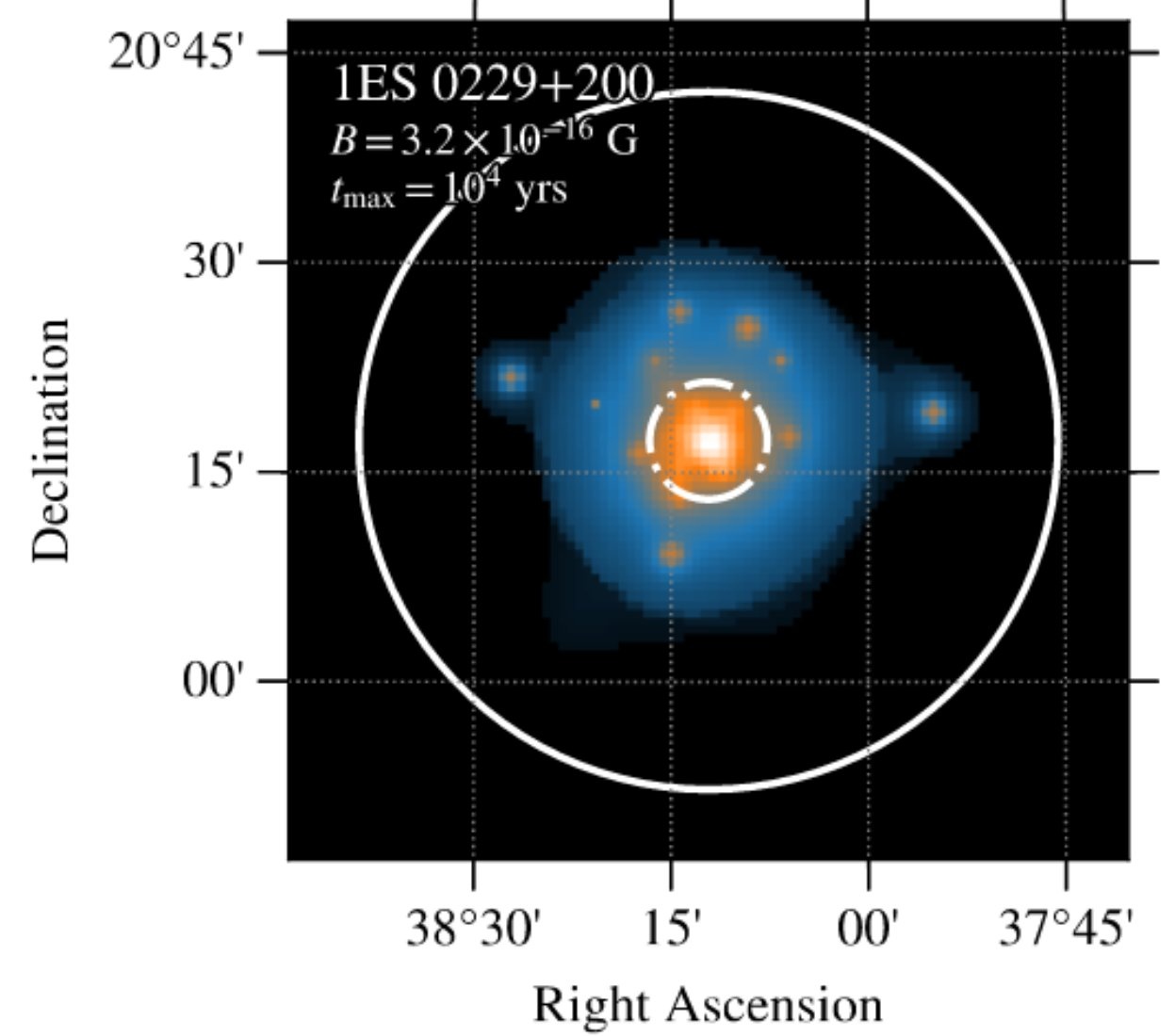
Observations of very high-energy gamma-rays, which are being studied with the H.E.S.S. telescopes have now been used to constrain the magnitude of the intergalactic magnetic field using a rather sophisticated technique. Just as antimatter and matter can annihilate into photons, an interaction of photons with energies above 1 GeV can annihilate into electrons and positrons. This phenomenon has been studied with the H.E.S.S. telescopes for several applications (see e.g. SOM 2013-08, SOM 2007-11). Very high energetic photons (at TeV energies) that interact with the low energy radiation of starlight that penetrate the universe will form very energetic electrons and these electrons, in turn, will Compton-scatter low energy photons to GeV energies, which will be observable as a distinct spectral and spatial component. A distant source of TeV photons is hence expected to be surrounded by a faint 'halo' (called pair-halo [1]). In case of a strong magnetic field, the electron-positron pairs will be significantly deflected from their initially straight propagation before they Compton-scatter ambient photons. The resulting pair halos are hence more extended (and fainter).
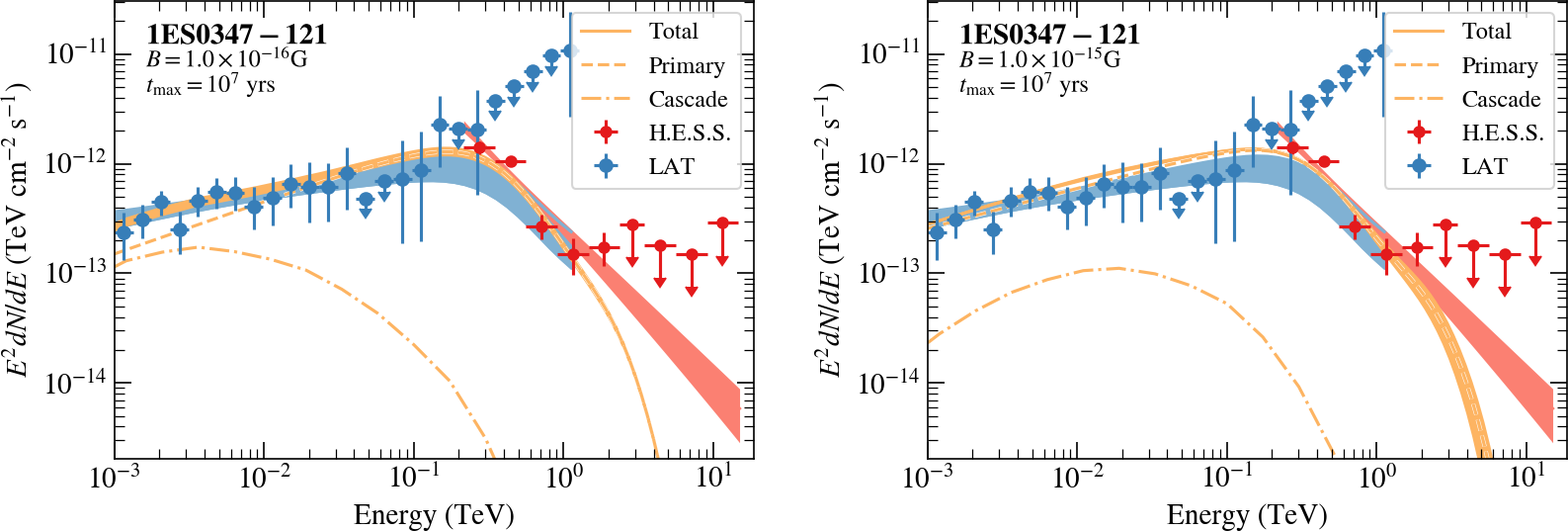
Observations with H.E.S.S. and the Fermi-LAT instrument have now been used to perform an updated search for the cascade emission of hard spectrum Blazars. A joint analysis of the observations with both instruments is used to construct the spectra in the 1 GeV - 10 TeV energy regime, and compute the amount of high-energy gamma-ray absorption caused by the pair creation. The amount of lower energy gamma-ray emission generated by the pair halo created by the pair creation process can then be predicted assuming a magnetic field of a a certain strength (see e.g. [2], [3]). At the same time, in image of the pair halo can be predicted for the assumed strength of the magnetic field. By comparing both, the predicted spectral shape and the predicted extension and brightness of the halo with the measurements, a limit on the required strength of the magnetic field can be computed even in case the halo as such cannot be observed. The H.E.S.S. and Fermi-LAT teams have now joined forces and derived the spectra and maps of 5 Blazars with very 'hard' spectra, which had been described as SOM 2005-12, SOM 2006-01, SOM 2007-10, SOM 2007-11 and SOM 2010-02. For each of the objects spectra were compared to models assuming different magnetic field (see fig. 1) and expected spatial distributions were simulated (see fig. 2). The pair halo emission - while unavoidable - cannot be identified spectrally or spatially and is thus constrained in surface brightness. This translates into a constraint on the strength of the cosmic magnetic field. The field must have a strength of at least 1.8 10^-14 (or 3.9 10^-14 ) G in case the Blazars observed are active for 10^4 (or 10^7) years respectively. This range of Blazar lifetimes correspond to expectations based on, e.g., the length of Blazar jets which are believed to be manifestations of Blazar activity.
References:
[1] Plaga, R. 1995, Nature, 374, 430
[2] Ackermann, M., Ajello, M., Baldini, L., et al. 2018, ApJS, 658 237, 32,
[3] Alves Batista & Saveliev, 2021, Universe, 7, 223
[4] HESS collaboration et al., 2023, submitted