Probing Lorentz symmetry at the Planck scale with Mrk 501
September 2018

Lorentz invariance is a pillar of special relativity and has been established to be an exact symmetry of Nature up to the precision of current experiments. However, the Lorentz symmetry could be broken at an energy scale that cannot be currently probed. Some quantum-gravity (QG) models postulate a foamy structure of spacetime near the Planck scale (1028 eV or 10-35 m), the scale at which spacetime would show quantum fluctuations which could affect the way high energy photons propagate in vacuum (see Figure 1 for an illustration). Namely, vacuum would exhibit a non-trivial refractive index due to the foamy structure of space time: as a consequence, photon propagation velocity would depend on the photon wavelength or, equivalently, on the photon energy. One may thus expect a break of the Lorentz symmetry at high energies [1]. A straightforward phenomenological approach to take into account for a possible Lorentz invariance violation (LIV) consists of adding extra terms in the dispersion relation of photons. The LIV effects are parameterized by a series of powers n of the photon energy divided by the Quantum Gravity energy scale EQG which is the quantity aimed to be measured or constrained. n=1 corresponds to a linear LIV effect, while n=2 corresponds to a quadratic LIV.
Although the Planck energy scale is extremely high and may seem out of reach of present day experiments, LIV would nonetheless leave distinctive signatures at lower energies. In particular, the propagation of high energy gamma rays in the universe could be affected in to ways: (i) the speed of propagation of gamma rays would be dependent on their energy, which would translate into an energy-dependent time delay in the arrival time of gamma rays traveling over astrophysical physical distances [2]; and (ii) the reaction threshold of their interactions would also be modified as a function of their energy [3,4], which would make the universe more transparent for high energy photons than it is with no LIV. In both cases, the higher the gamma-ray energy is, the more likely the effect is to be observable. The observation of very high energy gamma rays from blazars (a particular kind of active galaxy) allows to explore these two possible effects.
The strong flaring activity of the blazar Mrk 501 recorded by H.E.S.S. in June 2014 is a perfect opportunity to look for such LIV effects. H.E.S.S. data analysis reveals a rapid flux variability and an energy coverage extending from 1 TeV up to 20 TeV. These exceptional characteristics have been exploited to constrain the LIV energy scale using the two above-mentioned independent and complementary approaches.
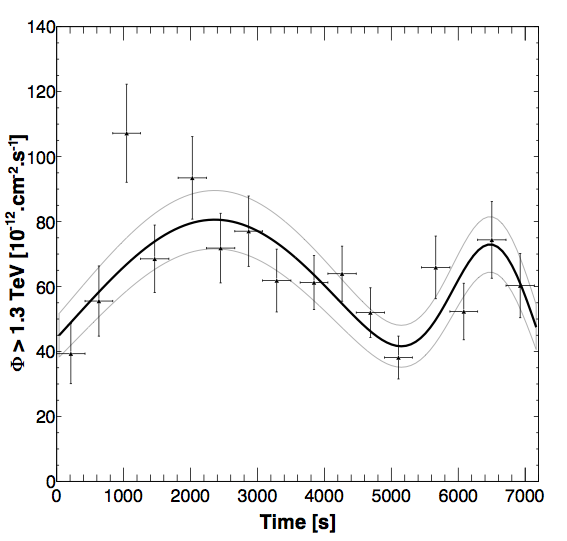
The temporal approach looks for an energy dependent time delay in the time evolution of the flux ('light-curve') during the flare. The observational data set are split into two energy range regions: a low-energy region is defined with energies between 1.3 and 3.25 TeV, while the high energy one makes use of energies higher than 3.25 TeV. The low-energy light curve is shown in Figure 2. Using a precise statistical method to measure the energy-dependent time delay, no significant energy-dependent lag in the arrival time of gamma rays is measured between the two regions [5]. This allows us to derive strong constraints on the energy scale of LIV, usually denoted as EQG due to its connexion with QG. The 95% confidence level upper limits on the energy scale EQG for the linear perturbation n=1 reaches 3.6x1017 GeV and 8.5x1010 GeV for the quadratic correction n=2, respectively. The latter value is among the best ever obtained with this type of effect.
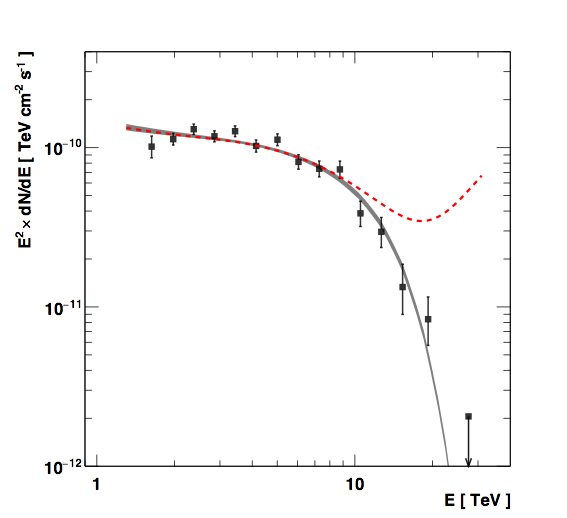
The spectral approach is based on the process of absorption of TeV gamma rays on their interaction with infrared photons of the extragalactic background light (EBL) - very high energy gamma rays interact with the infrared photons filling the extragalactic space creating electron positron pairs. The distance high energy photons can cross before being absorbed due to the EBL attenuation (the optical depth) has a specific energy and redshift dependence. In the presence of LIV, the perturbation in the dispersion relation propagates into the EBL optical depth. Indeed, the threshold of the pair production reaction is modified and the attenuation on the measured spectrum is affected. Optical depths to gamma rays using the EBL spectral energy distribution of the model of Franceschini et al. [6] can be computed considering modifications due to LIV for linear and quadratic perturbations, which would lead to an upturn in the spectrum in the subluminal case. For Mrk 501 (redshift z=0.034), EBL attenuation becomes significant at energies larger than 1 TeV and the flare detected in 2014 enables to evaluate this attenuation by precisely measuring its high energy spectrum. As shown in Figure 3, the Mrk 501 flare spectrum measured by H.E.S.S. is well fitted by an intrinsic power law attenuated on the EBL using the optical depth as modeled by Franceschini et al. [6]. The spectrum shows no significant evidence for an upturn in the spectrum, as would be observed in case of LIV. The non-observation of deviations with respect to standard EBL absorption in the energy spectrum of Mrk 501 allows H.E.S.S. to put constraints on the scale of LIV independently of the time-of-flight constraints. For the linear perturbation, 95% confidence level lower limit on EQG reaches 2.6x1019 GeV, i.e. a factor of two higher than the Planck scale, which is excluded at the 5.8 standard deviations level.
These constraints are amongst the best limits available in the literature, at the level of the limits obtained considering temporal effects with Gamma Ray Bursts. This demonstrates the crucial input of ground-based gamma ray astronomy to probe fundamental physics such as the search for Lorentz Invariance Violation at the Planck scale.
References:
[1] G. Amelino-Camelia, Living Rev. Rel. 16 (2013) 5
[2] G. Amelino-Camelia, J. Ellis, N.E. Mavromatos, D.V. Nanopoulos, S. Sarkar, Nature 393 (1998) 763
[3] F.W. Stecker, S.L. Glashow, Astropart. Phys. 684 16 (2001) 97
[4] U. Jacob, T. Piran, Phys. Rev. D 78 (2008) 124010
[5] H.E.S.S. Collaboration, H. Abdalla et al., to be submitted to Astrophys. J.
[6] A. Franceschini, G. Rodighiero, M. Vaccari, Astron. Astrophys. 487 3 (2008) 837