A Proton Accelerator? W49B Revisited
June 2016
Cosmic rays are high energy particles (mostly protons and atomic nuclei, but also a few electrons) that continuously hit the Earth from all directions. Since their discovery in 1912 by Victor Hess, the astrophysical sources of this cosmic radiation remains unclear, and one of the main goal of gamma-ray astronomy is to elucidate this mystery. Up to an energy of ~1015 eV (the so-called "knee" feature of the Cosmic ray energy spectrum), these particles are thought to be of Galactic origin. The strong shocks associated with the very energetic explosion that accompany the death of massive stars (so-called supernova remnants or SNRs) are good candidates to explain the origin of the hadronic component of these Galactic cosmic rays.
In order to validate this hypothesis, gamma-ray observations are a powerful tool, since particles accelerated at the SNR shock front radiate gamma rays with high- and very-high-energies. This emission can then be detected with satellite-based experiments like the Fermi-LAT or with ground-based instruments such as H.E.S.S. Depending on the nature of the accelerated particles (electrons or protons/nuclei), their spectral gamma-ray signature can be different. In the case of accelerated protons, or more generally hadrons, their interaction with the matter surrounding the astrophysical object produce neutral pions which rapidly decay in gamma rays. In this case, the expected gamma-ray spectrum has a very peculiar feature: a steep rise below ~200 MeV, often referred to as the "pion-decay bump".
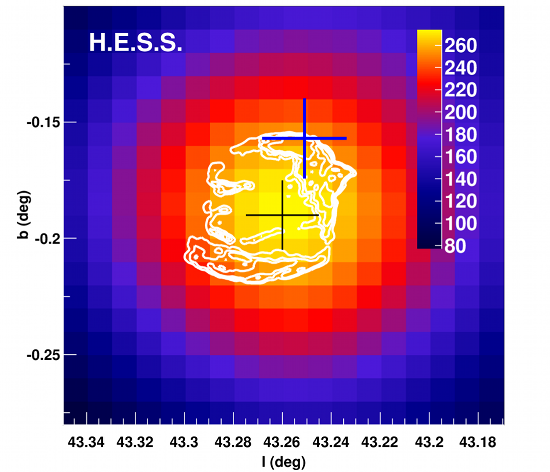
W49B (also known as SNR G43.3-0.2) is an object particularly interesting for the hunt for Galactic cosmic-ray accelerators. It is a rather young SNR (1000-4000 years), and its shock front is interacting with dense (103 particles/cm3) molecular material. The molecular cloud (MC) poses a dense target for hadronic interaction, and thus the gamma-ray emission from neutral pion decay is expected to be strongly enhanced. Such an SNR/MC association is therefore a good laboratory to test acceleration of protons and nuclei in SNRs.
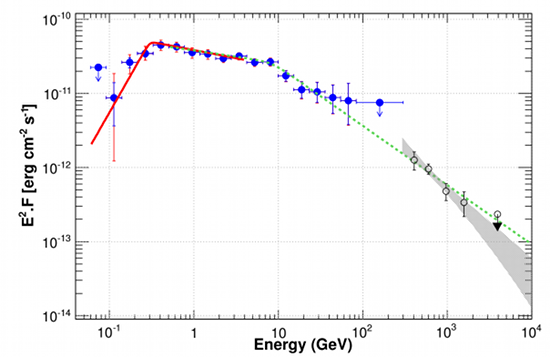
W49B is located ~10kpc away from the Sun in the Aquila constellation. VHE gamma-ray emission from this object has been first announced in 2010 by the H.E.S.S. Collaboration. Meanwhile, W49B has been observed for a total of 75 hours by H.E.S.S., and is now detected with a statistical significance of 13 standard deviations and a flux of roughly 0.6% of that of the Crab Nebula. Looking at this object at slightly lower energies, the Fermi-LAT collaboration published in 2010 a detailed study on this object, too [2]. Until today, 3 times more data has been recorded: due time for the Fermi-LAT and H.E.S.S. collaborations to work hand-in-hand to better understand this object (see [3] and figure 1). As can be seen in figure 2, the flux spectra measured by Fermi-LAT and H.E.S.S. are smoothly connected and show rather interesting spectral features. Firstly, a low-energy break is measured by the Fermi-LAT team, similar to those detected in the SNRs IC 443, W44 and W51C, and interpreted - for these sources - as the signature of gamma-ray emission produced through neutral-pion decay. Secondly, the joint spectral fit allows for the detection of a second spectral break at 8.4 GeV, similar to those observed in other SNR/MC associations. When confronting these results to model predictions, both hadronic and leptonic scenarios can explain the measured spectral shape. However, the sharp low-energy break detected at ~300 MeV seems to favor a hadronic origin.
Therefore, W49B is joining the very small club of SNRs in which we might be observing the acceleration of cosmic-ray protons and nuclei!
References:
[1] D.J. Helfand et al. MAGPIS: A Multi-Array Galactic Plane Imaging Survey. The Astronomical Journal (2006) 131, 2525.
[2] A. Abdo et al. Fermi-LAT Study of Gamma-Ray Emission in the Direction of Supernova Remnant W49B, The Astrophysical Journal 722 (2010) 1303.
[3] The H.E.S.S. and Fermi-LAT collaborations, "The supernova remnant W49B as seen with H.E.S.S. and Fermi -LAT", submitted to Astron. Astrophys., 2016.