Probing quantum gravity with TeV gamma rays
July 2010
Lorentz invariance states that the speed of light is identical in every reference frame, and for all photon energies. However, models of quantum gravity predict violations of Lorentz invariance. In quantum gravity, space-time aquires a structure on length scales of the Planck scale (10^-35 m), sometime referred to as a space-time foam. Directly probing these scales requires energies of the Planck energy scale, about 10^28 eV, far beyond all energies of particles produced in accelerators or observed in cosmic rays. However, even at much lower energies, such a hypothetical space-time foam may influence propagation of particles such as photons, modifying their speed of propagation. Particles will be more susceptible to effects of a space-time foam the shorter their wavelength is, and hence the higher their energy is. The modification of the speed of light is hence often parametrized as v = c (1-x E/M) or v = c(1- z (E/M)^2), where M is the Planck mass, and x or z serve to parametrize the strenght of the effect (e.g. Amelino-Camelia et al. 1998). Whether the effective speed depends linearly or quadratically (or not at all) on photon energy depends on the specific model of quantum gravity. Obviously, the effects are tiny; for x of order unity the speed of light changes one part in 10^16, comparing TeV photons with low-energy photons. One way to search for such variations is using flaring cosmic sources of gamma rays, where due to the large light travel time - 10^17 s for a source at Gpc distance - effects of quantum gravity might result in a detectable dispersion with energy of photon arrival times. To maximize sensitivity, flaring sources should provide a wide range of photon energies, be at cosmological distances, and provide short flares. Suitable sources are hence gamma-ray bursts and flaring active galaxies; using TeV gamma-ray data, first limits were obtained for Mkn 421 by the Whipple team (Biller et al. 1999); more recent results based on Mkn 501 data were reported by MAGIC (Albert et al. 2008). Using GeV gamma-rays from GRB 090510 at a redshift of 0.9, the Fermi team recently reported limits which probe the Planck scale (Abdo et al. 2009)
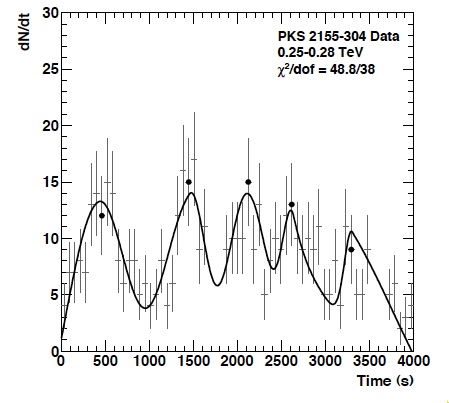
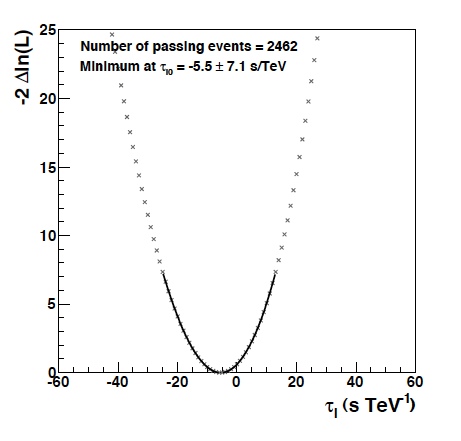
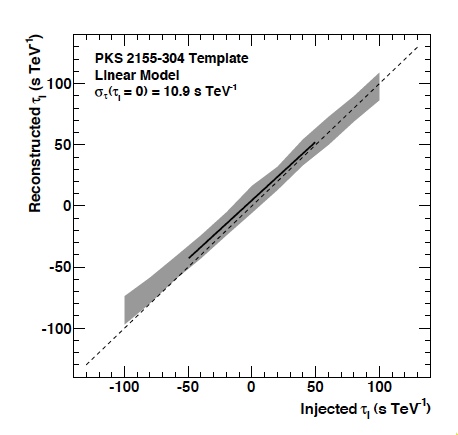
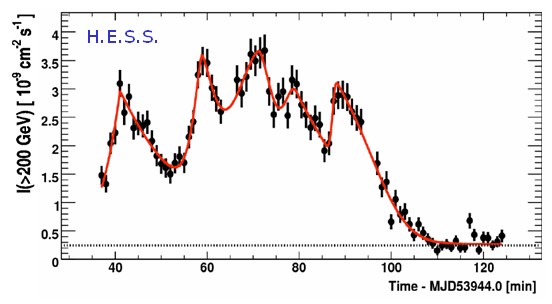
While no gamma-ray bursts were detected with H.E.S.S. so far (or with any other ground-based gamma-ray instrument), the huge flare of PKS 2155-304 in 2006 (see SOM 9/2007) provides a suitable burst source, at a redshift of 0.11. The outburst consisted of at least 5 distinct flares with risetime on the minute scale. A first search for effects of Lorentz violation was published by Aharonian et al. (2008), comparing the light curve in two distinct energy bins, from 200-800 GeV and above 800 GeV. Obviously, an analysis in two such coarse energy bins does not make optimum use of the information contained in the thousands of gamma-rays detected during the flare, with energies ranging up to several TeV. Therefore, an updated analysis has been untertaken, using in a likelihood fit the detailed information about the arrival time and energy of each individual photon, and adding an energy-dependent delay as a free parameter, following Martinez & Errando (2009). Fig. 1 shows, in a narrow energy band, the measured light curve and the analytical parametrization used to describe the light curve. Like the orginal analysis, the new analysis does not find an evidence for violations of Lorentz invariance, but the resulting limits are significantly improved. For the linear model, e.g., the likelihood that the data set is described by a given delay parameter is shown in Fig. 2; as a result, the arrival time is found to vary by -5.5+-7.1 sec per TeV energy, consistent with no dispersion and resulting in a limit on the mass scale of quantum gravity of about 2.1x10^18 GeV, or 17% of the Planck scale, the best limit obtained so far with TeV blazars. Extensive systematic tests were carried out calibrate the algorithm and to ensure that energy-dependent delays are properly reconstructed (e.g. Fig. 3). We note than all such limits rely on the assumption that there is no intrinsic variation of the gamma-ray light curve at the source, e.g. due to the acceleration mechanisms. Such intrinsic effects might fake or hide effects of Lorentz invariance variation. A positive detection would hence require demonstration that effects scale with source distance, and are hence related to photon propagation and not photon production.
Reference: "Search for Lorentz invariance breaking with a likelihood fit of the PKS 2155-304 flare data taken on MJD 53944", H.E.S.S. collaboration, A. Abramowski et al., submitted for publication